【摘要】介绍一种基于分位数优势估计（QAE）的强化学习新方法，通过重塑基线标尺，有效解决大语言模型训练中的熵值困境，实现稳定高效的性能提升。

引言

近年来，大语言模型（LLM）在复杂推理任务上的潜力日益凸显，尤其是在数学、编程等领域。为了引导模型从海量可能性中生成正确且逻辑严谨的答案，强化学习（RL）被广泛应用。然而，这条路径并非坦途。许多团队在实践中发现，基于强化学习的微调过程极不稳定，模型性能时常出现剧烈波动，甚至不升反降。这种现象的背后，潜藏着一个长期困扰研究者的核心难题——“熵值困境”。

熵，作为衡量系统不确定性的指标，在模型训练中扮演着双刃剑的角色。过高的熵意味着策略混乱，模型无法形成有效认知；过低的熵则代表思维僵化，模型丧失了探索新解法的能力。现有的训练方法，往往使模型在这两个极端之间摇摆，难以找到稳定的学习路径。本文将深入剖析这一困境的根源，并详细拆解一项由中科大团队提出的优雅解决方案——分位数优势估计（Quantile Advantage Estimation, QAE）。该方法通过对强化学习框架中一个基础组件的精巧重塑，仅用一行代码，便为动荡的训练过程装上了可靠的“稳定器”。

一、🧩 熵值困境：强化学习的隐形枷锁

在深入探讨解决方案之前，我们必须首先精确理解问题的本质。熵值困境并非单一问题，而是两种极端状态的统称，它们共同构成了强化学习微调（RLAIF/RLHF）过程中的主要障碍。

1.1 熵值崩塌（Entropy Collapse）

熵值崩塌，指的是模型策略分布的熵值过早、过快地下降，导致其行为模式高度固化。

可以将其想象成一个初学棋的AI。在训练初期，它可能会尝试各种开局。但如果在某次训练中，它使用“当头炮”恰好赢了几局，一个设计不佳的算法可能会过分奖励这一行为，导致模型迅速认为“当头-炮”是唯一的制胜法宝。从此，它在任何对局中都只会使用这一招，完全丧失了学习“仙人指路”或“起马局”等其他策略的能力。

在技术层面，这意味着模型的策略分布 π(a|s) 在某些动作 a 上的概率值迅速趋近于1，而在其他动作上的概率趋近于0。这种过早收敛到局部最优解的现象，对需要多步推理和创造性思维的任务是致命的。例如，在解决一个复杂的数学题时，可能存在多条解题路径。如果模型因早期偶然的成功而锁死在某一条路径上，当题目稍作变化，使其原有路径失效时，模型将束手无策。

熵值崩塌的直接后果是模型泛化能力的严重退化和创新性的完全丧失。

1.2 熵值爆炸（Entropy Explosion）

与熵值崩塌相对的，是熵值爆炸，即模型策略分布的熵值异常高企，行为输出趋于随机和无序。

这好比一个注意力涣散的学生，在解题时思绪天马行空。他可能一会试试公式A，一会又画个无关的辅助线，接着又开始心算一个完全不相干的数字。他的每一步尝试都毫无逻辑关联，最终无法形成连贯的解题步骤。

在技术上，熵值爆炸表现为策略分布 π(a|s) 趋向于一个均匀分布。模型对所有可能的下一个词元（token）都给予了差不多的概率，导致生成的文本序列逻辑混乱、语义不通。训练信号在这种高度随机的探索中被噪声彻底淹没，梯度更新失去了方向，模型无法从有效的尝试中学习，也无法从失败的尝试中吸取教训。

熵值爆炸使得训练过程难以收敛，模型无法学习到任何有意义的策略。

1.3 探寻根源：脆弱的“均值基线”

为何模型会在崩塌与爆炸之间剧烈摇摆？研究者发现，问题的核心症结在于当前主流强化学习算法中优势函数（Advantage Function）的估计方式，特别是其中基线（Baseline）的设定。

在策略梯度方法中，更新方向大致由下式决定：

∇θ J(θ) ≈ E[ ∇θ log πθ(at|st) * A(st, at) ]

其中，A(st, at) 是优势函数，它衡量在状态 st 下采取动作 at 比平均水平好多少。通常，它被定义为：

A(st, at) = Q(st, at) - V(st)

Q(st, at) 是动作价值（执行该动作后得到的期望回报），而 V(st) 是状态价值（在该状态下的平均期望回报），也就是我们所说的基线。引入基线的目的是为了降低梯度估计的方差，使训练更稳定。

在实践中，尤其是在处理一个批次（batch）的数据时，V(st) 常常被用该批次内所有样本奖励（rewards）的均值来近似。这便是问题的起点。

均值，作为一个统计量，对异常值（outliers）极其敏感。

让我们设想一个场景：在一个批次的100个解题尝试中，有99个得到了0分（解题失败），但有1个因为某种偶然因素（例如，模型碰巧生成了标准答案）得到了满分10分。

  • 传统均值基线：baseline = (99 * 0 + 1 * 10) / 100 = 0.1

  • 对于那99个失败的尝试，它们的优势值是 A = 0 - 0.1 = -0.1。这意味着它们都会受到惩罚，算法会试图降低生成这些序列的概率。

  • 对于那个成功的尝试，它的优势值是 A = 10 - 0.1 = 9.9。它会得到巨大的奖励。

表面上看似乎合理，但如果这99个失败的尝试中，有一些包含了部分正确的推理步骤，只是最终答案错了呢？这种“一刀切”的惩罚，会扼杀所有通往正确答案的中间探索路径，迫使模型只敢复现那个得到10分的“天选之子”路径，从而极易引发熵值崩塌。

反之，如果模型在某个阶段表现普遍较好，偶然出现一个极差的负分，均值基线被拉低，可能导致大量平庸的尝试也被判定为正优势，受到鼓励，从而使得策略发散，引发熵值爆炸。

下面的流程图清晰地展示了这一“污染”过程：

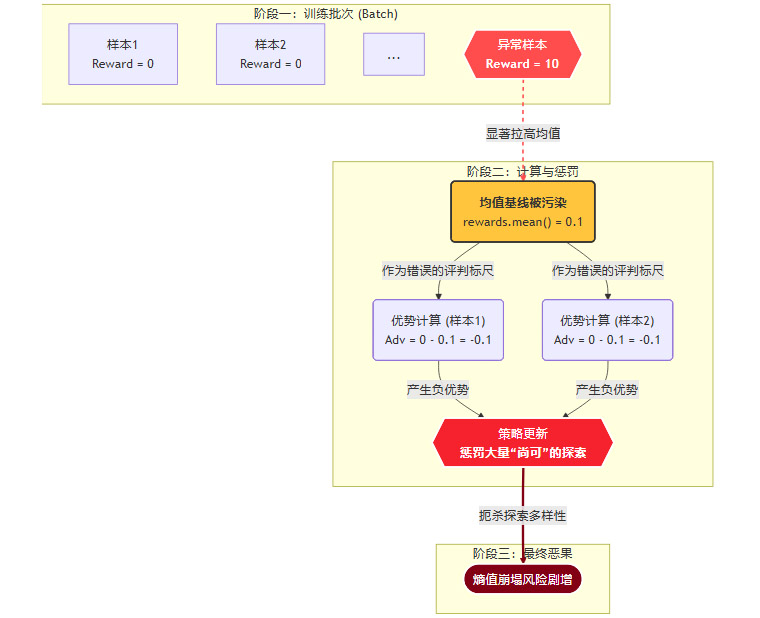
这种基于均值的脆弱标尺，是导致训练过程在两个极端间反复横跳的系统性缺陷。它无法公正、稳定地评估每一次尝试的价值，从而让整个学习系统陷入混乱。

二、⚖️ 重塑标尺：分位数优势估计（QAE）的原理与实现

既然问题的根源在于标尺本身，那么最直接的解决方案就是更换一把更精准、更稳健的尺子。中科大团队提出的**分位数优势估计（Quantile Advantage Estimation, QAE）**正是基于这一思想。

2.1 从均值到分位数：统计学的智慧

在统计学中，当数据分布存在极端值或偏斜时，**中位数（Median）或分位数（Quantile）**通常是比均值更可靠的集中趋势度量。

一个经典的例子是人均收入。假设一个城市有9个居民年收入10万元，1个富豪年收入1000万元。

  • 平均收入：(9 * 10 + 1 * 1000) / 10 = 109万元。这个数字显然不能代表普通市民的收入水平。

  • 中位收入：将所有人收入排序，取中间位置的数值，即10万元。这个数字更能反映真实情况。

分位数是中位数的推广。例如，25%分位数（Q1）意味着数据中有25%的值小于它，75%分位数（Q3）则意味着75%的值小于它。分位数的核心优势在于其稳健性（Robustness），它不受少数极端值的影响。

QAE方法正是将这种统计智慧引入到强化学习的基线设计中。它不再使用 rewards.mean()，而是使用 torch.quantile(rewards, q=τ) 作为基线，其中 τ 是一个介于0和1之间的分位数参数。

2.2 QAE的核心机制：智能门控

QAE的精妙之处在于，通过动态调整分位数参数 τ（或根据任务难度选择固定的 τ），它可以实现一种智能的“门控”机制，在不同场景下采取不同的评判策略。

我们可以将其类比为一位经验丰富的老师批改不同难度的作业：

2.2.1 场景一：攻坚难题（低成功率）

当模型面对一个非常困难的任务时，批次中的绝大多数尝试都会失败（奖励为0），只有极少数会成功（奖励为1）。

  • QAE策略：在这种情况下，选择一个较低的分位数，例如 τ = 0.2。由于大部分奖励都是0，那么20%分位数的值很可能就是0。

  • 基线设定：baseline = torch.quantile(rewards, q=0.2) ≈ 0。

  • 优势计算：

    • 对于失败的尝试（Reward=0）：Advantage = 0 - 0 = 0。它们不会受到惩罚。

    • 对于罕见的成功尝试（Reward=1）：Advantage = 1 - 0 = 1。它们会得到完整的正向奖励。

  • 效果：算法会集中火力强化那些极其宝贵的成功经验，同时对失败的探索保持“中立”，不予打击。 这极大地保护了模型的探索积极性，有效防止了因害怕失败而导致的熵值崩塌。这是一种“困难题重利用”的策略。

2.2.2 场景二：精通易题（高成功率）

当模型已经基本掌握一个任务时，批次中的大多数尝试都会成功（奖励为1），只有少数会失败（奖励为0）。

  • QAE策略：此时，选择一个较高的分位数，例如 τ = 0.8。由于大部分奖励都是1，那么80%分位数的值很可能就是1。

  • 基线设定：baseline = torch.quantile(rewards, q=0.8) ≈ 1。

  • 优势计算：

    • 对于成功的尝试（Reward=1）：Advantage = 1 - 1 = 0。它们不会再得到额外的奖励。

    • 对于少数的失败尝试（Reward=0）：Advantage = 0 - 1 = -1。它们会受到显著的惩罚。

  • 效果：算法的注意力会自动转移到那些仍然存在的错误上，进行精准“纠错”。 这避免了在已经掌握的技能上浪费计算资源，并推动模型向完美表现逼近。这是一种“简单题重纠错”的策略。

下表总结了QAE的智能门控机制：

场景

成功率

合适的 τ

基线 b_τ

优势计算（Adv）

核心目标

攻坚难题

低

较低 (如 0.2)

趋近于0

失败样本Adv≈0, 成功样本Adv>0

强化罕见成功，保护探索

精通易题

高

较高 (如 0.8)

趋近于1

成功样本Adv≈0, 失败样本Adv<0

聚焦残余错误，精准纠错

中等难度

适中

适中 (如 0.5)

介于0和1之间

平衡正负向更新

实现探索与利用的平滑过渡

2.3 一行代码的变革：工程实现

QAE最吸引人的一点在于其实现的极致简洁性。在现有的基于策略梯度的强化学习框架（如GRPO、DAPO等）中，开发者只需进行如下替换：

传统方法：

python：

# 使用均值作为基线

advantages = rewards - rewards.mean()

QAE方法：

python：

# 使用分位数作为基线

# tau 是一个超参数，例如 0.8

advantages = rewards - torch.quantile(rewards, q=tau)

这“一行代码”的修改，几乎不增加任何额外的计算开销。 分位数的计算需要对数据进行排序，其时间复杂度与排序算法相关（通常是 O(N log N)，N为批次大小），与计算均值（O(N)）在实际工程中差异不大，特别是对于现代硬件和并行计算库而言。更重要的是，它无需对复杂的算法流程进行伤筋动骨的改造，具有极强的即插即用特性。

2.4 理论保障：双向熵安全性

QAE的有效性不仅有直观的解释，更有严格的数学理论作为支撑。研究团队证明，在一阶软最大更新（first-order softmax update）的条件下，QAE能够为策略的熵值变化提供一个上下界，从而实现“双向熵安全性”。

这个理论保证可以通俗地理解为：

  • 防止熵值爆炸：在低成功率时，QAE通过将大量负优势样本的优势值置为0，有效抑制了大规模的负向更新，从而将策略的KL散度变化（即策略更新的剧烈程度）限制在一个很小的范围内，避免了策略的剧烈震荡。

  • 防止熵值崩塌：在高成功率时，QAE确保了对失败样本的惩罚，迫使模型继续调整策略，从而保证了策略更新的幅度，避免了模型过早停止学习、陷入局部最优。

这相当于为熵值的变化范围设定了一个动态的“安全护栏”，确保训练过程既不会“脱轨”也不会“熄火”，始终在一条稳定且高效的轨道上前进。

三、📊 实证分析：从数学推理到训练效率

理论的优雅最终需要通过实验来验证。研究团队在多个高难度数学推理基准上，对QAE方法进行了全面的评估。

3.1 实验设置

  • 测试基准：涵盖了多个极具挑战性的数学竞赛题库，包括美国数学邀请赛（AIME）2024/2025和美国数学竞赛（AMC）2023。这些任务需要模型具备多步、抽象的逻辑推理能力。

  • 模型规模：实验覆盖了80亿、140亿、300亿等不同参数规模的模型，以验证方法的可扩展性。

  • 对比基线：将QAE与使用传统均值基线的强化学习方法（如DAPO）进行直接对比。

3.2 性能提升：准确率与多样性的双赢

实验结果令人信服。QAE在所有测试模型和任务上都取得了显著的性能提升。

以80亿参数模型在AIME 2024测试集上的表现为例：

方法

pass@1 准确率

相对提升

pass@16 准确率

基线方法 (DAPO)

39.69%

-

70.11%

QAE (τ=0.8)

48.23%

+21.5%

70.11%

  • pass@1 准确率：指模型一次尝试就成功解题的概率。QAE将其从39.69%提升至48.23%，相对提升幅度高达21.5%。这是一个非常显著的进步，意味着模型的推理能力得到了实质性增强。

  • pass@16 准确率：指模型在16次尝试中至少有一次成功的概率，它衡量了模型生成解法多样性和潜在能力。QAE在大幅提升pass@1的同时，保持了pass@16的水平稳定。这说明性能的提升并非以牺牲探索多样性为代价，实现了准确性与多样性的“双赢”。

3.3 训练动态：更持久的学习能力

通过观察训练过程中的性能曲线，可以发现QAE与传统方法的另一个关键区别。

  • 第一阶段（协同增长期）：在训练初期，两种方法的性能都会提升。

  • 第二阶段（解耦平台期）：训练进行到后期，传统方法往往会很快进入一个性能平台期，准确率停止增长，甚至出现回落。而QAE方法则能够继续保持性能的稳步提升，展现出更持久的学习能力。

这表明，QAE通过更稳定的学习信号，帮助模型在训练后期依然能从数据中挖掘出有价值的信息，突破了传统方法的学习瓶颈。

3.4 效率奇迹：训练中的“二八定律”

在分析QAE的训练过程时，研究团队发现了一个非常有趣的现象：大约80%的训练样本被自动分配了零优势值（Advantage ≈ 0）。

这意味着，在每次参数更新中，只有约20%的“关键样本”真正驱动了模型的学习。这些关键样本，要么是罕见的成功案例（在攻坚期），要么是顽固的失败案例（在精通期）。

这一发现与著名的**帕累托法则（即“二八定律”）**不谋而合。QAE似乎天然地让模型学会了“抓重点”，将宝贵的计算资源集中在最有价值的20%样本上。

这带来了两大好处：

  1. 更高的训练效率：由于大量样本的梯度贡献为零，实际参与反向传播和参数更新的计算量减少了。这在一定程度上降低了算力开销，提升了训练吞吐量。

  2. 更强的抗噪声能力：通过自动过滤掉大量中性或信息量不足的样本，模型受到的噪声干扰更少，学习信号更纯净，从而更容易学习到正确的策略。

QAE的这种内在稀疏性，是其高效和稳定性的又一重保障。它证明了好的算法设计，能够引导系统自发地进入一种更经济、更高效的工作模式。

四、🌐 生态兼容性与行业视野

一个优秀的技术方案，不仅要自身性能卓越，还应具备良好的生态兼容性，能够融入现有的技术体系，并与其他方法协同工作。QAE在这方面表现出色。

4.1 与现有技术的互补关系

AI社区在解决训练稳定性问题上，已经从多个角度进行了探索。QAE的巧妙之处在于，它并非要取代这些方法，而是可以与它们形成强大的互补。

4.1.1 基线设计 vs. 正则项设计

我们可以将稳定训练的努力分为两大流派：

  • 正则项侧：这类方法通过在损失函数中添加额外的正则项来直接约束策略的熵。一个典型的例子是SIREN（Selective Information Regularization for ENtropy）。SIREN会选择性地对某些样本施加熵正则化，以防止策略过于集中。

  • 基线设计侧：这类方法，如QAE，则从问题的根源——优势函数的估计——入手，通过设计更稳健的基线来间接稳定熵。

QAE与SIREN等方法作用于算法的不同环节，因此完全可以组合使用。例如，可以使用QAE来提供一个稳定的优势信号，同时用SIREN来对策略的熵进行精细调控，从而达到1+1>2的效果。

4.1.2 兼容多种优化手段

无论是针对特定词元（token-level）的优化，还是针对整个序列（sequence-level）的优化，QAE都能无缝集成。因为它只改变了计算优势函数这一步，而优势函数是后续所有策略更新算法的共同输入。这意味着，无论上层使用的是何种RLVR（Reinforcement Learning from Verbal Reward）变体，QAE都可以作为其底层的“稳定基座”。

4.2 行业趋势：追求稳健的训练范式

放眼整个行业，对训练稳定性和反馈精准性的追求已成为共识。例如，一些研究开始探索RLPR（Reinforcement Learning from Process Reward），即不再仅仅根据最终答案的对错给予奖励，而是对解题过程中的每一步进行打分。这种过程监督的方式，提供了更细粒度的反馈信号，同样旨在提升学习的稳定性和效率。

QAE的成功，与这一宏观趋势是相符的。它证明了通过更智能、更稳健的统计方法来提纯和稳定学习信号，是提升复杂任务能力的关键路径。无论是改进基线设计（如QAE），还是优化奖励函数本身（如RLPR），其最终目标都是让模型在更可靠的指导下进行学习。

五、🔭 局限与未来展望

尽管QAE取得了显著成功，但它仍有进一步优化的空间。承认局限并思考未来，是技术持续进步的动力。

5.1 动态调整分位数参数 τ

当前版本的QAE大多采用一个固定的分位数参数 τ（例如，在实验中常用的 τ=0.8）。然而，一个固定的 τ 可能并非在整个训练过程中的所有阶段都是最优的。

  • 在训练初期，模型成功率很低，一个较低的 τ 可能更合适，以鼓励探索。

  • 随着训练的进行，模型成功率提高，一个较高的 τ 可能更优，以聚焦纠错。

因此，一个重要的未来方向是实现 τ 的自适应调整。可以设计一个调度器（scheduler），根据训练的实时状态来动态改变 τ 的值。可供参考的指标包括：

  • 成功率（Success Rate）：当批次成功率低于某个阈值时，降低 τ；高于时，则提高 τ。

  • 策略熵（Policy Entropy）：当熵值过低时，降低 τ 以鼓励探索；熵值过高时，提高 τ 以加强收敛。

  • 梯度方差（Gradient Variance）：监控梯度更新的稳定性，动态调整 τ 以最小化方差。

一个自适应的QAE，将使其“智能老师”的角色扮演得更加淋漓尽致。

5.2 推广至其他强化学习算法

QAE目前主要在基于策略梯度的RLVR框架下进行了验证。然而，其核心思想——使用稳健的统计量作为基线——具有很强的普适性。

另一个值得探索的方向是将QAE的思想推广到其他主流的强化学习算法中，例如PPO（Proximal Policy Optimization）。PPO是许多大规模LLM对齐训练（如RLHF）中使用的核心算法。将QAE的稳健基线设计与PPO的裁剪（clipping）机制相结合，有可能进一步提升对齐训练的稳定性和效果。

5.3 探索更复杂的基线模型

QAE用一个标量（scalar）的分位数替换了另一个标量的均值。更进一步，基线本身可以是一个更复杂的模型。例如，可以训练一个小的神经网络来预测给定状态 s 的价值 V(s)，并将其作为基线。在这种架构下，QAE的思想仍然可以被借鉴，例如，可以修改这个价值网络的训练目标，使其预测的不是奖励的期望值，而是奖励的某个分位数。

结论

回到我们最初的问题。大语言模型在强化学习中的“熵值困境”，本质上是一个由于评估标尺不准而导致的系统性失衡。传统均值基线这把“卷尺”，在面对复杂多变的训练数据时，显得过于脆弱和敏感。

中科大团队提出的分位数优势估计（QAE），则为我们提供了一把设计精良的“游标卡尺”。它通过引入稳健的分位数统计量，并巧妙利用其特性，实现了在不同学习阶段的自适应评判。这把新标尺，不仅用一行代码的代价，就为动荡的训练过程带来了久违的稳定，更在多个高难度任务上取得了实打实的性能飞跃。

QAE的成功，带给我们的启示是深刻的。在追逐更大模型、更复杂算法的浪潮中，我们有时会忽略那些构成系统基石的基础组件。这项研究提醒我们，回归基础，对那些看似理所当然的设定进行重新审视和优化，往往能以最小的代价，撬动最大的性能杠杆。

对于奋战在一线的AI工程师和研究者而言，QAE提供了一个立即可用、成本极低且效果显著的工具。而对于整个AI领域，这种“化繁为简”、从根本上解决问题的研究思路，或许比算法本身更有价值。随着QAE及类似方法的普及，我们有理由相信，未来的AI模型将不仅更“聪明”，也更“稳重”，能够在更多关键领域扮演可靠的智能伙伴。

📢💻 【省心锐评】

QAE用统计学的经典智慧，以一行代码的极简方式，优雅地解决了强化学习中的核心稳定难题。它证明了，最深刻的创新，往往源于对基础的重新思考。