【摘要】谷歌DQI算法通过将NP-hard优化问题巧妙转化为结构化的解码任务,利用量子干涉与经典解码协同,为特定难题开辟了超越经典计算的理论路径。
引言
在计算科学的版图中,组合优化问题始终占据着核心且极具挑战性的位置。从航空公司的航线规划、金融市场的投资组合优化,到新药研发的分子结构设计,这些问题不仅与商业效率息息相关,更直接影响着科学探索的边界。然而,其中绝大多数属于NP-hard(非确定性多项式时间困难)问题,其计算复杂度随问题规模呈指数级增长。这意味着,即便动用当今最强大的经典超级计算机,面对现实世界中的大规模实例时,寻找最优解依然是一项几乎不可能完成的任务。
这一困境自然而然地将希望投向了量子计算。数十年来,学界与业界一直在追问一个根本性问题,量子计算机究竟能否在经典计算彻底失效的优化领域取得决定性突破?尽管量子退火等启发式方法已在特定场景中有所应用,但要找到一种具备严格理论证明、能够提供指数级加速的通用量子优化算法,始终是该领域悬而未决的“圣杯”。随着容错量子硬件的曙光初现,对这一理论问题的探索已不再是纯粹的学术思辨,而是关乎未来计算架构和商业应用的紧迫议题。
在此背景下,谷歌量子AI团队联合多所顶尖学术机构,在《自然》杂志上发表了一项里程碑式的理论成果,提出了一种名为解码量子干涉(Decoding Quantum Interference, DQI)的新型量子算法。DQI的精妙之处在于,它彻底跳出了直接“求解”优化问题的传统思维框架,转而开辟了一条“转化”问题的新范式。它利用量子力学独特的干涉效应,将一个棘手的优化问题,映射为另一个同样困难但结构特性截然不同的解码问题,从而为利用经典计算领域数十年积累的强大解码工具打开了大门。这一思想的提出,不仅为特定优化问题带来了惊人的理论加速,更为我们理解和设计未来的量子算法提供了全新的视角和工具集。
❖ 一、DQI算法的核心机制:从“求解”到“转化”的范式革命

DQI算法的出现,标志着量子优化思路的一次重要演进。它不再执着于利用量子并行性对庞大的解空间进行暴力搜索,而是选择了一条更为迂回和智慧的路径,其核心在于问题域的战略性转移。
1.1 NP-hard问题的计算壁垒
要理解DQI的创新性,首先需要回顾经典计算在优化问题上面临的根本障碍。NP-hard问题最令人头疼的特性是其解空间的爆炸性增长。例如,一个仅有300个二元变量的简单优化问题,其可能的解组合数量就已超过宇宙中已知原子的总数。
经典算法,无论是精确算法还是启发式算法,在面对这种规模的搜索空间时都会遇到瓶颈。
精确算法(如分支定界法)虽然能保证找到最优解,但其运行时间在最坏情况下会呈指数增长,很快变得不切实际。
启发式算法(如模拟退火、遗传算法)能够在合理时间内找到一个不错的近似解,但无法保证解的最优性,且容易陷入局部最优的陷阱。
量子计算的早期愿景,如Grover搜索算法,虽然能提供平方级的加速,但对于指数级复杂度的NP-hard问题而言,这种加速仍然不足以带来质的改变。因此,量子优化领域亟需一种能够实现超多项式甚至指数级加速的新方法。
1.2 DQI的范式转移:优化即解码
DQI算法的革命性思想在于,它提出优化问题可以被重新表述为一个解码问题。这个过程可以类比为一个翻译任务,将一种难以理解的语言(优化问题的成本函数),翻译成另一种虽然也复杂但有成熟解读工具的语言(解码问题)。
这个解码问题,在数学上通常表现为最近向量问题(Closest Vector Problem, CVP)。我们可以用一个形象的例子来理解。
构建“格子”:想象在一个高维空间中,存在一个由一组基向量线性组合成的、规则排列的点阵,这便是“格”(Lattice)。每个格点都对应着优化问题的一个潜在解。
设定“目标”:优化问题的具体实例,可以被映射为这个高维空间中的一个“目标点”。
寻找“最近邻”:解码任务就是要在这个格点密布的空间中,找到距离该目标点最近的那个格点。这个“最近的格点”所对应的解,就是原始优化问题的近最优解。
DQI的巧妙之处在于,它设计的映射方式,使得原始优化问题的“最优解”恰好对应于解码问题中“距离最近的格点”。这样一来,一个复杂的寻优过程,就变成了一个几何空间中的寻近问题。
1.3 量子-经典协同:DQI的工作流程
DQI并非一个纯粹的量子算法,也不是一个纯粹的经典算法,而是一个深度融合的量子-经典协同框架。在这个框架中,量子计算和经典计算各自扮演着不可或缺且无法替代的角色。
1.3.1 量子计算的角色:干涉模式的构建者
量子计算机的核心任务是执行“转化”这一关键步骤。它并不直接输出解,而是通过一系列精密的量子门操作,制备一个特殊的量子态。这个量子态的特性在于,其概率幅分布经过了量子干涉的精心调控。
量子干涉:如同水波的相长和相消,量子算法可以设计出让指向“好解”(接近最优解)的计算路径相互增强,而让指向“坏解”的路径相互抵消的干涉模式。
概率放大:经过干涉后,对这个量子态进行测量,得到的结果会以更高的概率收敛到那些对应着近最优解的格点附近。
本质上,量子计算机在这里扮演了一个高效的“采样器”或“导航仪”,它利用量子效应,迅速将搜索范围缩小到高维空间中最有希望的区域,即目标点周围。没有量子干涉,要在指数级庞大的空间中高效定位这个区域是不可想象的。
1.3.2 经典计算的角色:高效的解码执行者
当量子计算机完成采样,给出一个靠近最优解的“目标点”后,接力棒就交到了经典计算机手中。此时,经典计算机的任务是执行一个高度专业化的问题,即格解码。
幸运的是,由于解码问题在通信(如5G、Wi-Fi)、数据存储(如DVD、二维码)和密码学等领域有着数十年的广泛应用,研究人员已经开发出大量针对特定结构格的高效经典解码算法。例如,针对具有代数结构的格(如里德-所罗门码),存在像Berlekamp-Massey算法这样极其快速的解码器。
DQI的整个工作流程可以用下面的Mermaid图来概括:
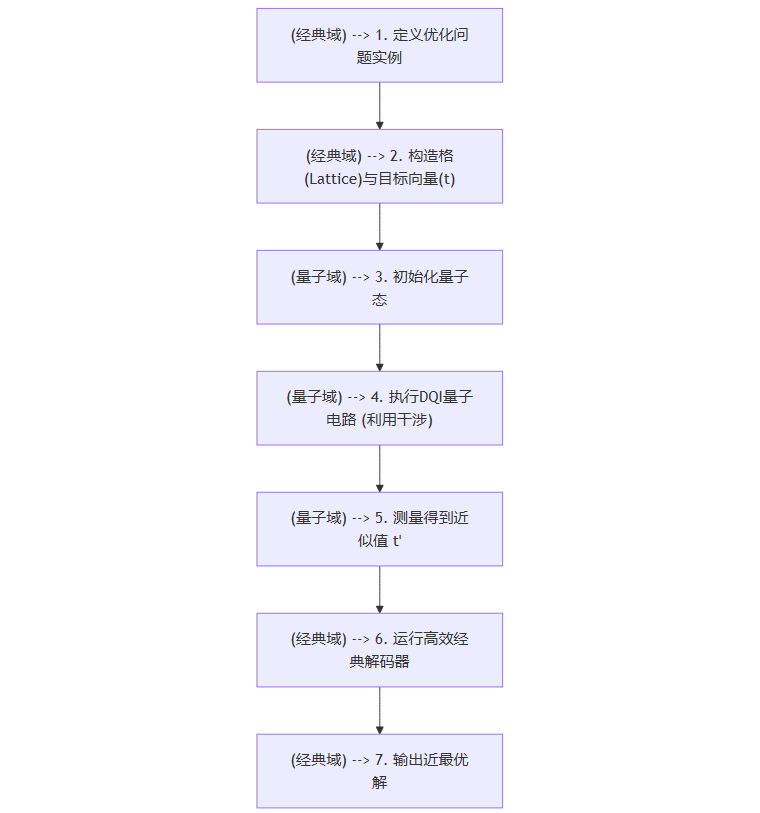
这个流程清晰地展示了DQI的混合计算范式。量子计算负责“指路”,经典计算负责“寻宝”。这种分工合作,使得DQI能够将量子计算的独特优势与经典计算的成熟算法积累完美结合,从而在特定问题上爆发出巨大的潜力。
1.4 从QUBO到格模型的统一视角
在深入DQI之前,有必要再审视一下当前量子优化领域的一个主流范式,即二次无约束二元优化(QUBO)。大量优化问题,从旅行商问题到蛋白质折叠,都可以被编码成QUBO形式。它的数学表达很简单,即最小化一个关于二元变量的二次型。
QUBO之所以流行,是因为它和物理上的伊辛模型(Ising Model)天然同构。量子退火机,例如D-Wave的设备,就是专门为求解这类问题设计的物理系统。变分量子算法(VQA)也常把QUBO作为目标哈密顿量。可以说,QUBO是连接组合优化与量子物理的一个核心桥梁。
DQI的思路则提供了一个不同的视角。它没有直接把问题映射到物理自旋系统,而是映射到了一个更抽象的几何结构,即格(Lattice)。QUBO关心的是能量基态,而DQI关心的是几何最近点。 这两种视角并非完全独立,某些QUBO问题也可以被表述为格问题,但DQI选择的路径更直接地对接了编码理论和代数几何,而不是统计物理。
这种选择的优势在于,编码理论经过几十年发展,已经形成了一套非常结构化的数学工具和高效算法。这些工具专门处理带有代数、组合或稀疏性质的结构。相比之下,求解通用QUBO问题的启发式算法,例如模拟退火,虽然普适,但在利用深层结构方面能力有限。DQI相当于用量子计算作为“扳手”,把优化问题撬开,暴露出其内在的、适合被编码理论工具处理的骨架。
❖ 二、OPI问题:DQI量子优势的标志性验证
理论的优美最终需要通过实例来证明其价值。在DQI的研究中,最优多项式交集(Optimal Polynomial Intersection, OPI)问题成为了展示其强大能力的第一个,也是最引人注目的“样板间”。
2.1 OPI问题剖析及其重要性
OPI问题在数学上可以这样描述:给定平面上的一系列数据点,以及一个次数上限 d,任务是寻找一个次数不超过 d 的多项式,使其能够穿过尽可能多的给定数据点。
这个问题是数据科学中多项式回归任务的一个变种,在许多领域都有着直接或间接的应用。
数据科学与机器学习:在处理含有大量离群点的数据集时,OPI可以帮助识别出最符合数据内在趋势的主体模式,是一种鲁棒性很强的拟合方法。
纠错码:在通信中,接收到的信号可以看作是带有错误(离群点)的数据点,找到正确的码字就等价于找到一个能穿过大多数“正确”点的多项式。
密码学:某些公钥密码系统的安全性也与解决类似多项式问题的难度相关。
尽管OPI问题描述简单,但它是一个典型的NP-hard问题。当数据点数量庞大时,暴力枚举所有可能的点子集并进行多项式拟合的计算量是无法承受的。
2.2 代数结构:量子优势的“非对称”来源
OPI问题之所以成为DQI的完美应用场景,关键在于其背后隐藏的深刻代数结构。当DQI将OPI问题转化为解码问题时,所生成的格并非一个随机、无序的点阵,而是一个具有特殊代数性质的格,这种格与里德-所罗门码(Reed-Solomon Code)的结构高度同构。
里德-所罗门码是一种在数字通信和存储领域应用极为广泛的纠错码,从光盘(CD/DVD)到二维码,再到深空通信,都能看到它的身影。经过几十年的发展,学术界和工业界已经为其设计出了一系列极其高效的解码算法。
这里的核心洞见在于一种“非对称性”。
对解码器友好:OPI问题内含的代数结构,使得转化后的解码问题变得异常“容易”,可以直接套用成熟的里德-所罗门解码器来快速求解。
对经典优化器不友好:然而,同样的代数结构,对于直接求解OPI问题的经典优化算法来说,似乎并没有提供任何捷径。经典算法仍然需要面对组合爆炸的困境。
量子计算机在这里扮演了“桥梁”的角色。它通过DQI算法,将经典优化算法无法利用的结构信息,传递给了经典解码算法,从而创造了专属于量子计算的优势空间。这在理论上首次清晰地回答了“量子优化能否超越经典”的疑问,给出了一个肯定的、可构造的实例。
2.3 惊人的理论性能鸿沟
DQI在OPI问题上展现的理论加速是颠覆性的。研究团队的复杂度分析给出了一个令人震撼的对比。
这个表格直观地展示了两者之间的巨大差距。10^23 是一个天文数字,远远超出了现有乃至可预见的未来任何经典计算机的处理能力。而几百万次的量子操作,对于一台未来的容错量子计算机来说,则完全在可行的范围之内。
这种从指数级到多项式级的复杂度降低,是量子计算追求的“圣杯”——量子优势的明确体现。它表明,对于OPI这类具有特定结构的问题,DQI不仅仅是提供了某种程度的加速,而是实现了从“不可计算”到“可计算”的质的飞跃。这一发现极大地增强了社区对于量子计算机在优化领域最终能够创造实际价值的信心。
2.4 列表解码与DQI的协同潜力
传统的RS解码算法,如Berlekamp-Massey算法或Euclidean算法,可以在错误数量不超过纠错能力上限(通常是(n-k)/2)时,唯一地恢复出原始多项式。但当错误数量超过这个阈值时,这些算法就会失效。
为了处理更高错误率的场景,Sudan和Guruswami等人发展了列表解码(List Decoding)算法。列表解码的目标不再是找到唯一的正确码字,而是输出一个包含所有与接收向量足够接近的码字的短列表。对于OPI问题来说,这意味着即使数据中存在大量“异常点”,列表解码仍然有可能把真正的“信号”多项式包含在输出列表中。
DQI与列表解码的结合具有巨大潜力。量子干涉过程可以将优化问题转化为一个高噪声环境下的解码实例,这恰好是列表解码算法的用武之地。DQI负责生成解码任务,而经典的、高度复杂的列表解码算法负责从噪声中捞出候选解。这种组合拳,使得DQI能够处理那些经典启发式算法在大量噪声干扰下容易陷入局部最优的OPI实例。量子部分负责全局结构的映射,经典部分负责代数层面的精细求解,二者分工明确,优势互补。
❖ 三、稀疏优化问题的挑战:量子优势的边界探索

在OPI问题上取得突破性成功后,一个自然的问题是,DQI的威力能否推广到更广泛的优化问题类别中?研究团队将目光投向了另一类在实际中应用极为普遍的问题——稀疏优化问题,并以max-k-XORSAT问题作为典型代表。
3.1 Max-k-XORSAT与LDPC码的连接
Max-k-XORSAT问题可以被看作是许多约束满足问题的基础模型。它的目标是找到一组二元变量的赋值,使得尽可能多的“异或”约束方程得到满足。这里的“k”表示每个约束方程最多涉及k个变量,“稀疏”的含义即k远小于总变量数。
这类问题在电路设计、人工智能、以及作为其他复杂优化问题(如Max-Cut、QUBO)的测试基准时都非常重要。DQI同样可以处理这类问题,其转化的路径如下:
转化目标:DQI将max-k-XORSAT问题转化为解码一种名为低密度奇偶校验码(Low-Density Parity-Check Code, LDPC)的问题。
结构对应:原始优化问题的“稀疏性”(每个约束只涉及少数变量),直接对应于LDPC码校验矩阵的“稀疏性”(矩阵中绝大多数元素为零)。
LDPC码是现代通信系统中性能最接近香non极限的纠错码之一,其解码算法也因其稀疏性而相对高效。因此,这条转化路径在理论上是通顺的。
3.2 “对称”的挑战:稀疏性的双刃剑
然而,在稀疏优化问题上,DQI遇到了与OPI问题截然不同的情况。这里的关键挑战在于,稀疏性这把“钥匙”可以被多方使用。
对DQI有利:稀疏性使得转化后的LDPC码解码问题变得更容易,这符合DQI的设计初衷。
对经典算法同样有利:问题的稀疏结构,也极大地帮助了经典的启发式算法,如模拟退火(Simulated Annealing)。模拟退火这类算法在处理具有局部结构或稀疏连接的问题时,性能会显著提升。
这就形成了一种“对称”的局面。DQI从稀疏性中获得的好处,在很大程度上被经典算法同样能利用这一特性所抵消。研究团队在论文中构造了一个精巧的max-k-XORSAT实例,在该实例上,DQI初步看起来比通用的模拟退火算法更有优势。但随后,他们又设计出一种专门针对该实例的、更强大的经典算法,再次追平甚至反超了DQI的表现。
这个过程揭示了一个深刻的道理:要宣称实现“量子优势”,必须确保所利用的问题结构是量子算法独享的,或者至少是经典算法难以利用的。在OPI问题中,代数结构形成了这种非对称优势。但在稀疏优化问题中,稀疏性带来的优势是普惠的,这使得确立明确的量子优势变得异常困难。
3.3 悬而未决的探索与新研究方向
目前,对于max-k-XORSAT这类稀疏优化问题,我们尚未找到一个明确的实例,可以被DQI高效解决,同时又能被证明无法被任何已知的经典算法高效解决。
但这并不意味着DQI在此类问题上毫无价值。相反,这一探索过程本身就极具启发性。
激发新算法:DQI的提出,促使研究人员从“解码”的视角重新审视优化问题,这可能会催生出全新的经典或量子启发式算法。
指导问题选择:它为寻找量子优势指明了方向,即需要寻找那些具有“非对称结构”的、对量子转化友好但对经典求解不友好的问题。
推动解码研究:DQI框架也为经典和量子的LDPC解码算法研究注入了新的动力,因为优化问题的需求可能会提出与传统通信场景不同的解码挑战。
因此,DQI在稀疏优化问题上的探索,更像是一次边界的勘探。虽然尚未发现宝藏,但绘制出的地图和积累的勘探经验,对于未来的寻宝之旅至关重要。
3.4 Tanner图与消息传递解码的视角
为了理解为什么稀疏性对经典解码和经典优化都有帮助,可以引入LDPC码的图表示——Tanner图。Tanner图是一个二分图,一侧的节点代表码字的比特位(变量节点),另一侧的节点代表校验方程(校验节点)。如果一个变量出现在某个校验方程中,就在对应的变量节点和校验节点之间连一条边。LDPC码的稀疏性,就体现在这个图的稀疏性上,即每个节点的度数都比较小。
LDPC的经典解码算法,如信念传播(Belief Propagation),正是在这个Tanner图上进行的消息传递过程。变量节点和校验节点之间来回传递“置信度”信息。变量节点告诉校验节点:“我认为自己是0或1的概率是多少”。校验节点收到所有相关变量的信息后,根据校验方程,计算并传回反馈:“基于其他人的信息,我认为你应该是什么值的概率是多少”。这个过程反复迭代,直到系统收敛到一个稳定的状态,从而完成解码。
稀疏性在这里至关重要,因为它保证了局部信息可以在图中有效传播而不会过早形成复杂的环路,使得迭代过程能够快速收敛。
现在回到max-k-XORSAT的经典优化。模拟退火、局部搜索等算法,其核心也是在变量之间进行局部调整。稀疏性意味着改变一个变量的值,只会影响到少数几个约束。这使得计算单步更新的成本很低,算法可以快速探索邻域。从这个角度看,经典优化算法的迭代过程,与Tanner图上的消息传递过程,在利用局部结构方面有异曲同工之妙。
因此,DQI在将max-k-XORSAT映射到LDPC解码时,虽然利用了稀疏性带来的解码便利,但这种便利性在经典优化端同样存在。这使得量子优势的窗口被大大压缩,需要找到那些“稀疏性恰到好处”的实例,才能体现出DQI的价值。
❖ 四、硬件要求与工程化落地挑战
DQI算法的理论光芒背后,是通往现实应用的一系列严峻的工程挑战。这些挑战主要集中在量子硬件、混合系统架构和软件生态三个层面。
4.1 大规模容错量子计算的现实距离
DQI算法的性能保证是建立在大规模、容错量子计算机的基础之上的。这意味着我们需要满足几个苛刻的条件:
足够多的量子比特:DQI处理有意义规模的问题,可能需要数千甚至数万个高质量的逻辑量子比特。
极低的错误率:算法涉及数百万次量子门操作,要求逻辑门的保真度极高,以防止计算过程中错误累积导致结果失效。
高连通性:量子比特之间需要有良好的连接性,以高效执行算法所需的复杂多比特门操作。
当前,我们仍处于“嘈杂中等规模量子”(NISQ)时代,量子比特数量有限,且容易受到环境噪声的干扰,错误率较高。从NISQ硬件到DQI所需的容错硬件,中间还有巨大的技术鸿沟需要跨越。
4.2 量子纠错开销与逻辑比特的现实
DQI所要求的“几百万门操作”是在逻辑量子比特(Logical Qubit)层面上的估算。一个逻辑量子比特是利用多个物理量子比特通过量子纠错编码(QEC)构建的、具有极低错误率的虚拟比特。当前主流的QEC方案,如表面码(Surface Code),其纠错能力与所用物理比特数量正相关。
为了构建一个错误率足够低的逻辑比特,可能需要数百甚至数千个物理量子比特。此外,在逻辑比特上执行一个逻辑门操作(如逻辑CNOT门),需要对底层的多个物理比特进行一系列复杂的、容错的门操作序列。这个从逻辑到物理的编译开销非常巨大。
因此,一个在逻辑层面需要一百万门的DQI算法,翻译到物理层面,可能需要数十亿甚至更多的物理门操作,并且需要一个拥有数万到数百万物理量子比特的、高度稳定的量子芯片。这是当前硬件水平无法企及的。DQI的理论优势,必须放在这个巨大的工程开销背景下进行评估。 它更像是一个远期的技术灯塔,指明了容错时代量子计算机的一个杀手级应用方向,但通往那里的道路依然漫长。
4.3 软件栈与编译器的挑战
实现DQI这样的混合算法,对量子计算的软件栈也提出了极高要求。
高级语言与编译器:需要一种能够描述复杂混合算法的编程语言,编译器不仅要能将量子部分编译成脉冲序列,还要能高效地处理量子与经典之间的控制流和数据交换。
资源估算与优化:在算法设计阶段,就需要精确的资源估算工具,能够预测一个DQI实例在特定硬件架构下需要多少逻辑比特、多深的电路以及总运行时间。编译器需要进行深度优化,例如通过门重排、并行化等手段,压缩电路规模。
运行时系统:需要一个低延迟的运行时系统来调度量子处理单元(QPU)和经典处理器(CPU/GPU)。DQI可能需要在一个循环中多次调用QPU和经典解码器,二者之间的数据通路必须高效。任何延迟都会严重影响算法的整体性能。
这些软件层面的挑战,其难度不亚于硬件本身。一个强大的软件生态,是连接DQI这样的理论算法与未来物理硬件的必要桥梁。
❖ 五、DQI 对算法设计思想的启发

超越具体的算法实现,DQI的提出为整个量子算法设计领域带来了更深层次的哲学思考和范式启发。
5.1 从单体算法到混合系统
DQI的成功,标志着量子算法设计思想的一次重要演进。早期量子算法,如Shor算法和Grover算法,更像是“单体应用”,即整个核心计算过程都封闭在量子计算机内部完成。而DQI从设计之初就是一个深度耦合的量子-经典混合系统。
它清晰地划分了量子和经典的职责边界:
量子计算:负责利用叠加和干涉,完成经典计算难以胜任的“结构变换”和“概率放大”。它不负责找到最终答案,而是生成一个“更容易解决的”中间问题。
经典计算:负责执行那些经过数十年优化、高度成熟的确定性算法(如解码算法),对量子计算生成的中间问题进行高效求解。
这种设计范式更具工程可行性。它承认了量子计算的优势是局部的、专用的,而不是普适的。未来的量子应用,很可能都不是纯粹的量子程序,而是以量子协处理器的形式,嵌入到更大的经典计算流程中,专门解决其中的某个计算瓶颈。
5.2 结构优先的问题筛选范式
DQI还为寻找量子优势问题提供了一个新的筛选标准,即“结构不对称性”。一个问题是否适合用DQI解决,关键看它是否具有某种深层结构(如代数结构或稀疏结构),并且这种结构满足:
可以被量子算法利用,将其映射到一个高效可解的经典问题(如解码)。
这种结构本身,不能被已知的经典算法直接利用来简化原始问题。
这个标准比单纯看问题的计算复杂度(如是否为NP-hard)更具指导意义。它要求算法设计者不仅要懂量子计算,还要对经典算法的边界、编码理论、代数几何等领域有深入理解。未来的量子算法研究,可能会出现更多这样跨领域的交叉。研究人员会从各个应用领域中,主动寻找那些具备“结构不对称性”的“宝藏问题”。
5.3 量子与经典算法的协同进化
DQI的出现,也可能反过来促进经典算法的发展。正如论文中所示,当DQI在某个稀疏优化问题上表现出优势时,它立刻激励研究人员去设计更强的、针对该结构的经典算法。这种“军备竞赛”是良性的。
量子算法为经典算法设定了新的性能标杆。如果一个量子算法声称在某类问题上有优势,它就为经典算法社区提供了一个明确的挑战目标。
经典算法的进步反过来提高了量子优势的门槛。这会迫使量子算法研究者去寻找更难以被经典模拟的量子特性,或者去攻克结构更复杂的问题。
长远来看,量子计算和经典计算不是简单的替代关系,而是一种协同进化的关系。DQI开辟的这条“优化-解码”路线,为这种协同进化提供了一个绝佳的试验场。
结论
谷歌提出的解码量子干涉(DQI)算法,为“量子计算能否解决实际优化问题”这一核心议题,提供了一个迄今为止结构最清晰、理论最扎实的肯定回答。它没有沿用传统的量子搜索或退火范式,而是开创性地将复杂优化问题转化为格解码问题,通过量子干涉扮演“结构转换器”的角色,让经典世界几十年积累的高效解码算法得以在新的战场上发挥作用。
在最优多项式交集(OPI)问题上,DQI与里德-所罗门解码的结合,展示了惊人的理论加速潜力。其背后利用的“结构不对称性”——即问题的代数结构能被解码器利用,却难以被经典优化器直接利用——为寻找量子优势提供了一个可复制的范式。这不仅是一个漂亮的理论成果,更是一个明确的信号,标志着量子优化研究从宽泛的复杂度分析,走向了针对特定问题结构的精准打击。
而在稀疏优化领域,DQI与LDPC解码的探索则揭示了这条道路的复杂性。稀疏性对量子和经典算法的双重助益,使得量子优势的窗口变得狭窄,并激发了经典算法的针对性反击。这恰恰反映了技术发展的真实面貌,即量子优势并非一蹴而就,而是在与不断进化的经典算法的持续博弈中艰难确立的。
从工程角度看,DQI的落地依赖于遥远的大规模容错量子计算机,其巨大的硬件开销和复杂的软件栈挑战不容忽视。然而,它的价值并不局限于远期应用。DQI所体现的量子-经典深度混合、结构优先的问题筛选、以及二者协同进化的设计哲学,已经对当下的算法研究和系统架构产生了深远影响。它告诉我们,未来的量子计算生态,将是一个量子与经典各司其职、紧密协作的异构系统。
对于身处技术浪潮中的我们而言,DQI的启示是双重的。一方面,它为量子计算的应用前景描绘了一幅具体而可信的蓝图;另一方面,它也强调了跨领域知识融合的重要性。理解量子力学、优化理论和编码理论的交集,将是抓住下一轮计算变革机遇的关键。
📢💻 【省心锐评】
DQI把量子优化从玄学拉回结构工学,谁能先把自家业务问题映射到“可解码”的好结构,谁就更有机会在量子时代占到先手。

.png)


评论