【摘要】Error-Free Linear Attention (EFLA) 通过求解常微分方程的解析解,替代了传统线性注意力中的数值近似,从根本上消除了离散化误差,为大模型处理超长序列提供了前所未有的数值稳定性。

引言
在大型语言模型领域,上下文长度的扩展一直是核心议题。标准的Transformer架构,其自注意力机制的计算与存储开销随序列长度 L 呈 O(L²) 的平方关系增长。这一特性构成了模型处理长文档、长对话或进行复杂推理时的根本性计算瓶颈。为了突破这堵“二次方墙”,学术界与工业界提出了多种近似方案,其中线性注意力(Linear Attention)因其将复杂度降至 O(L) 而备受瞩目。
线性注意力的核心思路是将注意力计算重构为一个动态的、可在线更新的记忆状态。然而,效率的提升往往伴随着精度的妥协。现有主流的线性注意力实现,其更新规则在数学本质上多为对一个底层连续过程的离散化近似,其中最常见的是一阶欧拉法。这种近似在短序列上表现尚可,但当序列长度剧增或输入信号能量较大时,离散化所引入的局部截断误差会持续累积,最终导致数值不稳定与记忆“漂移”,严重损害模型在长程依赖任务上的表现。
针对这一根本性缺陷,南洋理工大学的雷靖迪、复旦大学的张迪以及南洋理工大学的波利亚·苏佳妮娅在一篇编号为 arXiv:2512.12602v1 的研究中,提出了名为 “无误差线性注意力”(Error-Free Linear Attention, EFLA) 的全新范式。这项工作没有在改进近似方法的道路上继续前行,而是回归问题的数学本源,将线性注意力的更新过程建模为常微分方程(ODE),并利用其动力学矩阵的特殊结构,求得了该方程的 解析解(Analytical Solution)。这一转变,意味着将注意力的更新从一个充满累积误差的近似步进,升级为一个在理论上完全精确的积分过程,从而在不增加计算复杂度的前提下,彻底解决了长序列场景下的稳定性难题。
🎯 一、线性注意力的瓶颈与数值困境
%20拷贝-znby.jpg)
要理解EFLA的价值,必须先审视当前线性注意力技术路线所面临的内在矛盾,即计算效率与数值精度之间的权衡。
1.1 标准自注意力的计算高墙
标准自注意力机制的强大之处在于其能够捕捉序列中任意两个位置之间的依赖关系。它通过计算查询(Query)与所有键(Key)的点积相似度,并进行Softmax归一化,得到注意力权重,最后对值(Value)进行加权求和。其计算可以形式化地表示为:
Attention(Q, K, V) = softmax(QKᵀ / √dₖ)V
其中 Q, K, V 分别是维度为 L × d 的矩阵。核心的计算瓶颈在于 QKᵀ 这一步,它需要计算一个 L × L 的注意力矩阵,导致了 O(L²d) 的时间复杂度和 O(L²) 的空间复杂度。当序列长度 L 从数千扩展到数万甚至百万时,这种平方增长的开销变得无法承受。
1.2 线性注意力的承诺与隐忧
线性注意力的目标是打破这种平方依赖。其核心技巧在于通过一个核函数 φ(·) 替换Softmax,使得注意力的计算顺序可以交换:
Attention(Q, K, V)ᵢ = (Σⱼ φ(Qᵢ)ᵀφ(Kⱼ)Vⱼ) / (Σⱼ φ(Qᵢ)ᵀφ(Kⱼ))
通过交换求和顺序,可以先计算 Σⱼ φ(Kⱼ)Vⱼᵀ 和 Σⱼ φ(Kⱼ),这两个量可以被看作是累积的“记忆状态”。对于一个自回归模型,在解码第 t 步时,记忆状态可以从第 t-1 步递归更新而来:
Sₜ = Sₜ₋₁ + φ(Kₜ)Vₜᵀ
Zₜ = Zₜ₋₁ + φ(Kₜ)
Attentionₜ = (φ(Qₜ)ᵀSₜ) / (φ(Qₜ)ᵀZₜ)
这种递归形式将每一步的计算复杂度稳定在 O(d²),总复杂度为 O(Ld²),实现了对序列长度的线性扩展。这极大地提升了模型处理长序列的效率。然而,这种看似完美的方案,其稳定性却埋下了隐患。许多先进的线性注意力变体,如引入遗忘门控的机制,其更新规则可以抽象为:
Sₜ = f(Sₜ₋₁, Kₜ, Vₜ)
这里的更新函数 f,在许多实现中,等价于对一个更底层的连续动态过程的离散化模拟。
1.3 潜藏的缺陷:数值离散化的累积误差
EFLA研究团队通过深入分析发现,许多带有遗忘机制的线性注意力更新规则,其数学本质可以追溯到一个连续时间的常微分方程(ODE)。例如,一个带指数衰减的记忆更新过程可以被描述为:
dS(t)/dt = -βS(t) + K(t)V(t)ᵀ
这是一个描述记忆状态 S(t) 如何随时间 t 连续演化的方程。在数字计算机中,我们处理的是离散的序列数据(token by token),因此需要将这个连续过程离散化。最简单直接的方法就是一阶前向欧拉法(First-Order Forward Euler Method)。
使用欧拉法,在时间步长为 Δt 的情况下,状态 Sₜ 的更新近似为:
Sₜ ≈ Sₜ₋₁ + Δt * (-βSₜ₋₁ + Kₜ₋₁Vₜ₋₁ᵀ)
这正是许多现有线性注意力(如DeltaNet中的delta规则)更新形式的来源。欧拉法虽然计算简单,但其内在缺陷是它只是一阶近似。每一步都会引入一个 O(Δt²) 的局部截断误差。当序列长度 L 非常长时,总的累积误差可以达到 O(LΔt²)。这意味着序列越长,最终的状态与真实积分结果的偏差就越大。
这种误差累积在以下几种情况下会急剧恶化:
长序列场景:步数
L巨大,误差累积效应显著。高能量输入:当键
Kₜ的范数很大时,系统的动态变化非常剧烈(即所谓的“刚性”问题),一阶近似会产生巨大偏差,甚至导致数值发散。大学习率:在训练中,较大的学习率相当于增大了离散化的步长,放大了截断误差。
这个根本性的数值缺陷,是导致现有线性注意力模型在长程依赖任务上表现不佳、稳定性差的核心原因。它们就像是用一把刻度粗糙的尺子去测量一条蜿蜒的海岸线,距离越长,测量的结果就越不可靠。
🎯 二、EFLA的核心思想:从动力学视角求解精确更新
EFLA的贡献在于它没有试图去寻找一个更高阶、更复杂的近似方法(比如二阶或四阶龙格-库塔法),而是直接求解了问题的精确答案。
2.1 范式转换:将更新建模为常微分方程
EFLA的第一步,是正式地将线性注意力的在线更新过程定义为一个连续时间动力学系统。其状态 S(t) 的演化由以下常微分方程描述:
dS(t)/dt = -Aₜ S(t) + bₜ
S(t)是d × d的记忆状态矩阵。Aₜ = kₜkₜᵀ是由当前步的键向量kₜ构成的动力学矩阵,它控制着记忆的衰减模式。bₜ = kₜvₜᵀ是输入项,代表当前步的新信息。
这个方程描述了在接收到新信息 (kₜ, vₜ) 后,记忆状态 S(t) 将如何变化。
2.2 连接离散与连续:零阶保持假设
由于输入数据 (kₜ, vₜ) 是以离散的token序列形式到达的,需要一个假设来连接离散输入和连续动力学。EFLA采用了在数字控制系统中广泛使用的**零阶保持(Zero-Order Hold, ZOH)**假设。
ZOH假设认为,在一个离散时间步长 β(可以看作一个可学习的参数或超参数)内,输入信号 kₜ 和 vₜ 保持恒定。这个假设物理意义明确,使得在每个时间区间 [t-1, t] 内,上述ODE的系数 Aₜ 和 bₜ 都是常数。对于常系数线性ODE,其解是存在且唯一的,并且有明确的积分形式。
从 t-1 时刻的状态 Sₜ₋₁ 演化到 t 时刻的状态 Sₜ,其精确解可以通过积分得到:
Sₜ = e^(-βAₜ)Sₜ₋₁ + ∫[0,β] e^(-(β-τ)Aₜ)bₜ dτ
这个公式是精确的,没有任何近似。它由两部分组成:
e^(-βAₜ)Sₜ₋₁:代表旧有记忆Sₜ₋₁经过时间β的衰减后的状态。∫...:代表在时间段β内,新输入bₜ对系统产生的累积影响。
现在,问题转化为了如何高效地计算矩阵指数 e^(-βAₜ) 和后面的积分项。
2.3 数学突破口:动力学矩阵的秩-1结构
直接计算通用矩阵的指数和积分是极其昂贵的,通常需要 O(d³) 的复杂度,这会使线性注意力的优势荡然无存。然而,EFLA的关键洞察在于,这里的动力学矩阵 Aₜ = kₜkₜᵀ 并非任意矩阵,它是一个秩-1(Rank-1)矩阵。
一个秩-1矩阵具有非常优美的代数性质:
特征值:它只有一个非零特征值
λₜ = kₜᵀkₜ = ||kₜ||²,其余d-1个特征值均为零。对应的特征向量就是kₜ。幂次性质:对于任意整数
n ≥ 1,有Aₜⁿ = (||kₜ||²)^(n-1) Aₜ。
利用这些性质,矩阵指数的泰勒级数展开可以被极大地简化:
e^(-βAₜ) = I + Σ[n=1,∞] ((-β)ⁿ/n!) Aₜⁿ
= I + Σ[n=1,∞] ((-β)ⁿ/n!) (λₜ)^(n-1) Aₜ
= I - (1/λₜ) (Σ[n=1,∞] ((-βλₜ)ⁿ/n!)) Aₜ
= I - (1/λₜ) (e^(-βλₜ) - 1) Aₜ
= I - (1 - e^(-βλₜ))/λₜ * Aₜ
这个推导的最终结果是惊人的。原本需要无穷级数求和的复杂矩阵指数运算,被转化为了一个只涉及标量指数函数 e^(-βλₜ) 的简单闭式表达式。这把计算的复杂度从矩阵级别降到了标量级别。
同样,利用 Aₜbₜ = (kₜkₜᵀ)(kₜvₜᵀ) = kₜ(kₜᵀkₜ)vₜᵀ = λₜbₜ 的关系,积分项也可以被精确计算出来:
∫[0,β] e^(-(β-τ)Aₜ)bₜ dτ = ( (1 - e^(-βλₜ))/λₜ ) * bₜ
将这两部分精确解组合起来,就得到了EFLA的最终更新规则:
Sₜ = (I - αₜkₜkₜᵀ)Sₜ₋₁ + αₜkₜvₜᵀ
其中,αₜ = (1 - e^(-β||kₜ||²)) / ||kₜ||² 是一个由键向量范数决定的动态标量。
🎯 三、EFLA的实现与性能分析
%20拷贝-svsd.jpg)
EFLA的理论优雅性必须转化为工程上的可行性。其设计在保持数学精度的同时,充分考虑了计算效率和硬件兼容性。
3.1 计算复杂度:精度无需代价
尽管EFLA的更新公式看起来比简单的欧拉法更复杂,但其计算复杂度并未增加。我们来分解一下每一步的计算:
计算键范数的平方
λₜ = ||kₜ||²:O(d)计算标量衰减因子
αₜ:O(1)计算
kₜkₜᵀSₜ₋₁:可以按kₜ(kₜᵀSₜ₋₁)的顺序计算,复杂度为O(d²)。计算
kₜvₜᵀ:外积,复杂度为O(d²)。组合结果:矩阵加法和标量乘法,复杂度为
O(d²)。
因此,每一步更新的总时间复杂度依然是 O(d²),整个序列的处理复杂度为 O(Ld²),与标准的线性注意力完全一致。EFLA实现了理论精度的提升而无需付出额外的计算代价。
3.2 工程可行性:并行化与硬件兼容
现代深度学习的性能高度依赖于GPU的并行计算能力。EFLA的更新规则在代数结构上与DeltaNet等模型高度兼容,这意味着为这些模型开发的**分块并行(Chunk-wise Parallel)**计算策略可以无缝迁移。
分块并行计算的基本思想如下:
将长度为
L的序列划分为大小为C的块。在每个块内部,并行计算所有token的键、值以及它们对块内记忆状态的贡献。
块与块之间,串行地传递和更新累积的记忆状态。
下面是一个简化的流程图,展示了这一过程:
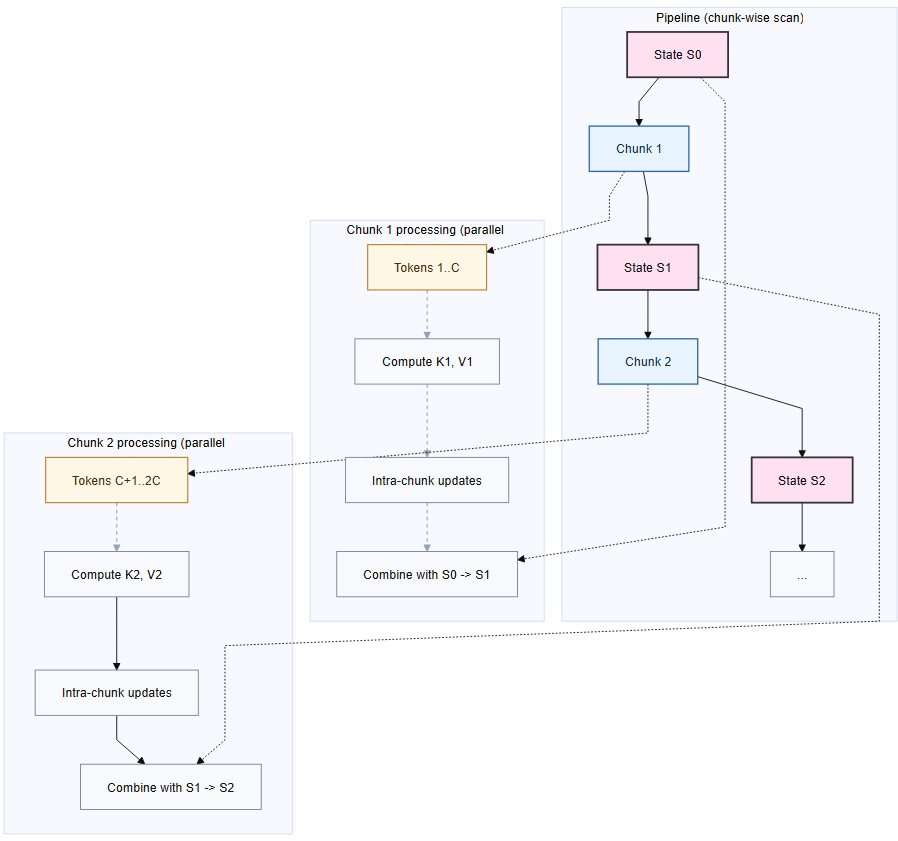
这种实现方式能够充分利用GPU的并行核心,使得EFLA在实际部署中能够达到与现有高效线性注意力相当的吞吐量,证明了其不仅理论优美,也具备强大的工程落地潜力。
3.3 数值稳定性:告别离散化误差
EFLA的核心优势在于其无与伦比的数值稳定性。从数值分析的角度看,不同的积分方法对应不同的精度。
EFLA相当于使用了一个无穷阶的龙格-库塔方法,它给出的不是近似值,而是数学上的精确积分结果(在浮点精度范围内)。这意味着由离散化引入的误差源被彻底根除。无论序列多长、输入信号多强,更新过程本身不会成为不稳定的来源。这为构建能够稳健处理百万级甚至更长上下文的模型奠定了坚实的数学基础。
🎯 四、EFLA的内在机制与理论洞察
EFLA的数学形式不仅带来了稳定性,还揭示了线性注意力更深层次的工作机制,特别是关于记忆如何被动态地管理和塑造。
4.1 动态门控:键向量范数的自适应调节作用
EFLA更新规则的核心在于标量因子 αₜ = (1 - e^(-β||kₜ||²)) / ||kₜ||²。这个因子由键向量 kₜ 的范数平方(即能量)||kₜ||² 所决定,扮演着一个**动态门控(Dynamic Gate)**的角色。
我们可以分析 αₜ 的行为:
当
||kₜ||²→ 0 时(弱信号):
利用泰勒展开e⁻ˣ ≈ 1 - x,我们有αₜ ≈ (1 - (1 - β||kₜ||²)) / ||kₜ||² = β。
此时,EFLA的更新规则退化为:Sₜ ≈ (I - βkₜkₜᵀ)Sₜ₋₁ + βkₜvₜᵀ
这正是标准的delta规则更新形式,也是欧拉法的一阶近似。这表明,传统的线性注意力只是EFLA在输入信号非常弱的非刚性条件下的一个特例。当
||kₜ||²→ ∞ 时(强信号):
指数项e^(-β||kₜ||²)趋近于0,因此αₜ ≈ 1 / ||kₜ||²。
更新幅度受到键能量的抑制,呈现出一种饱和效应。
这种自适应行为至关重要。它意味着EFLA能够根据输入信息的重要性(以键的能量来衡量)来智能地调整其记忆更新策略:
对于强信号(重要的、高能量的输入):系统会进行一次显著的更新,衰减因子
1 - αₜkₜkₜᵀ会更强烈地作用于旧记忆,有效地为新信息“腾出空间”。对于弱信号(次要的、低能量的输入):系统更新幅度较小,更倾向于保留历史上下文。
这种机制确保了模型在面对不同强度输入时的鲁棒性,避免了在遇到异常值或高能量token时因过度更新而导致的灾难性遗忘。
4.2 方向性遗忘:基于谱分解的精准记忆擦除
EFLA的记忆衰减项 e^(-βAₜ) = I - αₜAₜ 不仅是自适应的,还是方向性的。由于 Aₜ = kₜkₜᵀ 是一个秩-1矩阵,它的作用可以用谱分解来清晰地理解。
矩阵 Aₜ 只有一个非零特征值 λₜ = ||kₜ||²,其对应的特征空间由向量 kₜ 张成。其余所有与 kₜ 正交的向量都位于 Aₜ 的零空间中。
因此,当衰减算子 e^(-βAₜ) 作用于前一时刻的记忆 Sₜ₋₁ 时:
对于
Sₜ₋₁中与kₜ对齐的分量:这部分记忆会按照e^(-βλₜ)的因子被指数衰减。这是一个强烈的遗忘过程。对于
Sₜ₋₁中与kₜ正交的分量:这部分记忆完全不受影响,被完整保留。
直观地看,EFLA实现了一种精准的、方向性的记忆管理。每当一个新的信息 (kₜ, vₜ) 到来时,系统会首先识别出与新信息键 kₜ 最相关的历史记忆方向,然后精确地、按指数级衰减该方向上的旧信息,为新信息 kₜvₜᵀ 的融入创造条件。而与新信息无关的记忆维度则得到保留。
这就像一个高效的图书管理员,当一本新书入库时,他不会把整个书架清空,而是只精确地找到与新书主题最相关的旧书区域,进行整理和更新,而其他区域的书籍则保持原样。
4.3 训练动态观察:稳定性与收敛速度的权衡
EFLA的精确积分特性虽然带来了无与伦比的稳定性,但也引入了独特的优化动态。其更新强度由饱和函数 αₜ 控制,这导致了与线性响应的delta规则不同的行为。
训练早期:梯度通常较大且充满噪声。EFLA的饱和效应此时扮演了一个鲁棒滤波器的角色,可以有效抵御高方差梯度和异常值的干扰,防止模型因不稳定的更新而发散。这使得EFLA在训练初期表现得非常稳定。
训练后期:当模型接近收敛时,特征逐渐变得明确,某些键的范数
||kₜ||²可能会变得很大。此时,饱和效应会抑制这些高置信度特征的更新幅度,导致梯度信号被指数级压缩,类似于一种“梯度消失”现象。这可能会减缓模型在细粒度优化阶段的收敛速度。
这种稳定性与响应性之间的权衡是EFLA设计的内在特性。为了应对这一挑战,研究团队发现,EFLA通常需要配合相对较大的全局学习率。较大的学习率可以补偿指数饱和带来的更新抑制,使模型在饱和状态下依然保持对新信息的响应能力,同时又不损失其理论上的无误差保证。
🎯 五、实验验证与性能收益
%20拷贝-oyor.jpg)
理论的优雅最终需要通过实验来证明其价值。EFLA的研究团队设计了一系列全面的实验,从数值稳定性和语言建模两个维度验证了其有效性。
5.1 数值稳定性压力测试
为了验证EFLA在极端条件下的鲁棒性,研究者在序列MNIST任务上进行了压力测试,引入了多种干扰:
输入信号放大:将输入像素值乘以一个放大因子。
高斯噪声:向输入添加不同强度的高斯噪声。
随机丢失:随机将部分像素置零。
实验结果清晰地表明:
随着扰动强度的增加,基于欧拉近似的DeltaNet性能出现断崖式下跌,证实了其在高能量和噪声输入下的脆弱性。
EFLA在所有扰动条件下均保持了极高的准确率,展现出卓越的鲁棒性。尤其是在使用较大学习率训练时,EFLA的优势更加明显,这与理论分析中的饱和效应和稳定性相符。
5.2 语言建模与零样本推理任务
在更具挑战性的语言建模任务上,研究团队在Wikitext等数据集上对EFLA进行了评估,并在一系列零样本常识推理任务(如LAMBADA, PiQA, HellaSwag等)上测试了其性能。
为了确保公平比较,EFLA采用了与基线模型(如DeltaNet)完全相同的模型架构和训练预算。实验结果显示:
整体性能提升:在绝大多数任务上,EFLA都超越了基线模型。例如,在对长程依赖要求很高的LAMBADA任务上,EFLA不仅显著降低了困惑度,还将准确率提升了数个百分点。在BoolQ任务上,准确率提升甚至达到了7.4%。
信息保真度的体现:这些性能提升直接证明了“更准确的记忆更新”可以转化为实际的任务表现。通过消除离散化误差,EFLA能够更忠实地保留和利用长序列中的历史信息,从而做出更准确的预测。
可扩展性验证:在使用1.3B参数模型和更大规模数据进行训练时,EFLA的性能优势依然存在,并且有随着训练进行而进一步扩大的趋势,验证了该方法的可扩展性。
这些实验结论有力地支撑了EFLA的核心价值:它不仅在理论上是精确的,在实践中也能带来实实在在的性能收益。
结论
EFLA(Error-Free Linear Attention)为长上下文大模型的发展提供了一个坚实且优雅的数学基础。它通过将线性注意力的更新过程从一个充满误差的欧拉近似,升级为一个在理论上完全精确的解析解,从根本上解决了困扰现有线性注意力方法的数值稳定性问题。
这项工作的核心贡献在于,它揭示了利用深度学习模型中特定组件的**代数结构(如秩-1)**来寻找精确解的可能性。这代表了一种从“追求更好的近似”到“利用结构获得精确计算”的范式转变。EFLA证明了,我们可以在不牺牲计算效率的前提下,获得理论上的最优精度,为构建能够稳健处理百万级甚至更长序列的下一代AI模型铺平了道路。对于开发者和架构师而言,EFLA不仅是一个可直接应用的优化方案,更是一种启发性的设计哲学,鼓励我们在未来的模型设计中,更多地去发掘并利用问题本身的数学之美。
📢💻 【省心锐评】
EFLA用解析解替换数值近似,根治了线性注意力的长序列“漂移”顽疾。它不是又一个近似技巧,而是回归数学本源的降维打击,为超长上下文AI的稳定性提供了理论最优解。

.png)
%20%E6%8B%B7%E8%B4%9D-neng.jpg)

评论